Eine mathematische (online)-Entdeckungsreise rund ums Parkett: Enrichmentangebote für begabte Schüler:Innen in Zeiten von Covid-19

In der Schule lernen wir Mathematik häufig als eine Ansammlung von Kochrezepten kennen, bei denen es meistens um das Anwenden von Formeln und das Ausrechnen von Dingen geht. Wie kommen wir aber auf solche Formeln? Sie müssen entdeckt werden. An dieser Stelle geht es also nicht mehr um das Anwenden, sondern um die Forschung. Auch wenn Mathematik eine sehr alte Wissenschaft ist und somit auch schon vieles diesbezüglich entdeckt wurde, so forschen dennoch täglich tausende WissenschaftlerInnen in der Mathematik, um mehr über sie zu erfahren. Und es geht dabei um weit mehr als bloß um Formeln. Das Forschen ist also ebenso unzertrennlich mit der Mathematik verwoben wie eben auch mit anderen Wissenschaften. Im Schulunterricht kommen das eigene Forschen und Entdecken aber oftmals zu kurz. Gerade besonders motivierte, begabte oder leistungsstarke SchülerInnen können darunter leiden, dass der Unterricht nicht genügend Futter liefert oder dass vermeintlich übermäßige Neugier auf Unverständnis trifft.

Mit den Begabungs(co)piloten fördert die Claussen-Simon-Stiftung seit 2017 Enrichment-Kurse an Hamburger Schulen und erweitert damit die Begabungspiloten-Initiative. Seit 2017 sucht Deutschland in diesem Programm nach neuen Möglichkeiten, leistungsstarken SchülerInnen eine angemessene Förderung zu bieten. Diese Bemühungen haben nicht den Zweck, denen, die schon viel haben, noch mehr zu geben, sondern den SchülerInnen bedürfnisorientiert die Aufmerksamkeit zu geben, die sie verdient haben. 

Ganz konkret bin ich mit Dr. Karl Heuer und Kerrin Bielser gerade dabei, einen Online-Mathematik-Enrichment-Kurs in diesem Rahmen durchzuführen. Die Teilnehmenden sind SchülerInnen aus Hamburger Stadteilschulen und Gymnasien. Dabei sind SchülerInnen aus durchweg allen Klassenstufen von Klasse 6 bis Klasse 10 vertreten. Hierbei schöpfen wir drei aus langjähriger Erfahrung als Kursleitende und TutorInnen im Förderprogramm der William-Stern-Gesellschaft, insbesondere im Sekundarstufenbereich, und seit Neuerem auch im PriMa-Projekt. Das Ganze hätte eigentlich vor Corona – und natürlich offline stattfinden sollen. Für die SchülerInnen ist es online noch viel schwieriger, in der Gruppe LernpartnerInnen zu finden. Auch das Mikrofon in einer Videokonferenz anzuschalten, stellt eine psychische Barriere dar, die im realen Klassenraum nicht vorkommt. Andererseits bietet ein Onlinekurs viel einfachere Vernetzungsmöglichkeiten über Schulgrenzen hinweg.

Was geschieht nun aber genau in unserem Onlinekurs? Jeden Samstag gibt es ein Aufgabenblatt, das den Teilnehmenden per E-Mail zugesendet wird. Zu Beginn der folgenden Woche gibt es dann die Möglichkeit, offene Fragen, meistens zum Verständnis, in einer Videokonferenz zu klären. Am Ende der Woche werden dann die Ergebnisse ausgetauscht. Zwischenzeitlich nutzen einige Kinder die digitale Infrastruktur, um in kleinen Arbeitsgruppen gesondert Videokonferenzen abzuhalten. Andere schreiben uns fleißig E-Mails oder rufen uns an. Für uns TutorInnen ist es ein Mehraufwand an Flexibilität; würden wir uns auf die Videokonferenzen beschränken, würde viel Raum für Rückmeldung fehlen. Wir können nicht verlangen, dass alle Teilnehmenden ein Gerät haben, mit dem sie gut in den Videokonferenzen arbeiten können, angefangen bei einer Webcam. Deshalb müssen wir uns auch bis zu einem gewissen Grad auf die Eltern verlassen, die zuhause nachhaken, falls es Probleme gibt. 

In unseren Kursen arbeiten wir in sogenannten offenen Problemfeldern. Wir wollen hier den Kindern ermöglichen, sich als Forschende zu probieren. Was meinen wir genau mit einem offenen Problemfeld? Um eine genaue Definition muss ich mich hier drücken. Offen heißt aber gewiss nicht ohne Regeln. Wichtig ist, dass die SchülerInnen auf Entdeckungssuche gehen können, sich eigene (Folge)probleme überlegen, über Lösungen reflektieren, aber auch – und dies ist besonders wichtig, wenn wir mathematisch begabte SchülerInnen im Klassenverband fördern wollen – entsprechend ihrer Begabungen und Interessen Exkurse vornehmen können, die entweder tiefer mathematisch sind oder aber in die Gesellschaft oder in Kunst oder Kultur reichen. Neben der Vermittlung von mathematischen Inhalten und Methoden setzen wir vor allem auf eigenständiges und intrinsisch motiviertes Arbeiten und wollen dazu beitragen, eine höhere Frustrationstoleranz zu erreichen. Gerade Letzteres ist sehr wichtig, denn wir alle haben in der Regel ein ganz bestimmtes Bild von Begabten vor Augen, die sich nicht beirren lassen von Sackgassen oder Fehlern. Doch gerade, wenn einem Vieles zufällt, ist es wichtig, auch mit Situationen konfrontiert zu sein und mit diesen gut umzugehen, in denen nicht der gleich alles gelingt oder eindeutig ist und in denen man durchhalten muss. 

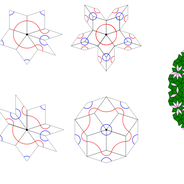
In diesem Kurs haben wir uns konkret mit Parkettierungen beschäftigt. Wir alle haben Parkette und Fliesen in vielfältigen Formen um uns. Und einmal für das Thema sensibilisiert, findet man überall spannende Muster dieser Art. Zum Beispiel der Hundertwasser-Bahnhof in Uelzen, der Boden der Hamburger U-Bahn-Station Saarlandstraße oder der Boden der Laeiszhalle. An das, was man aber beispielsweise in der Alhambra in Granada bestaunen kann, reichen diese Fundstücke vielleicht nicht ganz heran. Solche kleinen Exkurse in Kunst und Kultur haben wir auch in unserer ersten Woche unternommen, und sie kamen bei den Teilnehmenden gut an. Der mathematische Part beginnt aber mit der Frage, welche regelmäßigen n-Ecken es zulassen, mit ihnen den Boden lückenlos und ohne Überlappungen auszulegen, wenn wir nur eine Sorte von n-Ecken verwenden. Wer darüber ein bisschen nachdenken möchte, sollte hier kurz pausieren.

Allen anderen verraten wir gerne sofort, dass man dies alleinig mit 3-, 4- und 6-Ecken erreichen kann. Um dies zu beweisen, muss man auf die Idee kommen, die Innenwinkel eines n-Ecks zu berechnen, um zu prüfen, ob diese Winkel den Vollwinkel, also 360° teilen. Und in der Tat sehen wir beispielsweise bei regelmäßigen Dreiecken, dass ihre Innenwinkel 60° betragen, also ein Sechstel von 360°. Beispiele für zugehörige Parkette sind schnell gefunden. Eventueller Übermut oder vielleicht auch noch nicht antrainierte Gründlichkeit lassen einen gerne schnell vergessen zu beweisen, dass dies auch tatsächlich alle Möglichkeiten sind. Aber dafür sind wir TutorInnen da. Nicht, um Methoden in die Köpfe zu trichtern, sondern um Hinweise zu geben und noch einmal nachzuhaken, ob ein Argument tatsächlich das beweist, was behauptet wurde. 

In den Problemfeldern geht es zusätzlich darum, nicht einfach aufzuhören, wenn man einen Erfolg erzielt hat, sondern sich eigene Probleme zu stellen. Wie wäre es, wenn ich für ein Parkett mehrere Arten von n-Ecken kombiniere? Welche n-Ecken können einen dreidimensionalen Körper bzw. Raum formen bzw. begrenzen? Warum sollten die n-Ecken eigentlich regelmäßig sein, geht es nicht auch mit anderen Formen? Sehen alle Parkettierungen periodisch aus? … Auch nach über zehn Jahren Kursarbeit mit begabten SchülerInnen treten immer wieder neue Fragen auf. Eine kleine Übersicht von Möglichkeiten haben wir hier zusammengestellt^{1, 2}. Neben dem Generieren neuer Fragen sehen wir es für unsere Teilnehmenden als wichtig an, dass auch die sozialen Komponenten der Mathematik erkannt werden. Es geht auch darum die Gruppe zu überzeugen, MitstreiterInnen zu finden, besonders aber darum, das Verstandene gut zu kommunizieren und sich dabei präzise auszudrücken.

Mit den Sommerferien vor der Tür geht nun auch langsam unser Onlinekurs erstmal in die Sommerpause. Trotz, oder gerade wegen der widrigen Umstände ist es erstaunlich, wie schnell sich die SchülerInnen an die neue Situation anpassen konnten. Mit viel Durchhaltevermögen und hoffentlich noch viel mehr Spaß haben sie eine Tür zur Mathematik und dem Umgang mit ihr geöffnet, die sonst vielleicht noch länger verschlossen gewesen oder eventuell gar nicht geöffnet worden wäre.

Referenzen

Die Materialien sind frei verfügbar. Eine größere Sammlung (auch zu anderen Themen als Parketten) gibt es hoffentlich im kommenden Jahr, 2021 bei Springer unter dem Titel „Forschend Mathematik erleben“. Bis dahin wird aber hoffentlich auch noch mehr kostenfrei im Netz zugänglich sein.

[1] W. Bedenknecht, K. Heuer und D. Sarikaya (MS) Förderung mathematisch begabten Jugendlicher innerhalb des Klassenverbandes am Beispielaufgabenfeld der Parkettierung der Ebene. Online verfügbar

[2] K. Heuer und D. Sarikaya (2019). Group theory via symmetries for enrichment classes for gifted youth. In: M. Nolte (Ed.): Including the Highly Gifted and Creative Students – Current Ideas and Future Directions Proceedings of the 11th International Conference on Mathematical Creativity and Giftedness (MCG 11). p. 257 - 263. Online verfügbar